O que é a sequência de Fibonacci?
Essa sucessão de números, descrita no século 12, está presente em muitas coisas do nosso cotidiano, dos cartões de crédito aos girassois. Veja como.

A sequência de Fibonacci sucessão de números que aparece codificada em muitos fenômenos da natureza. Descrita no final do século 12 pelo matemático italiano Leonardo Fibonacci, ela é infinita e começa com 0 e 1. Os números seguintes são sempre a soma dos dois números anteriores. Portanto: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34…
Os termos da sequência de Fibonacci estabelecem entre si a chamada proporção (ou razão) áurea, muito usada na arte, na arquitetura e no design por ser considerada agradável aos olhos. Seu valor é de 1,618… Trata-se de um número irracional, infinito, representado na matemática pela letra grega phi: φ.
Quanto mais você avança na sequência de Fibonacci, mais a divisão entre um termo e seu antecessor se aproxima desse número. Veja só:
2 ÷ 1 = 2
3 ÷ 2 = 1,5
5 ÷ 3 = 1,666…
8 ÷ 5 = 1,6
13 ÷ 8 = 1,625
21 ÷ 13 = 1,615
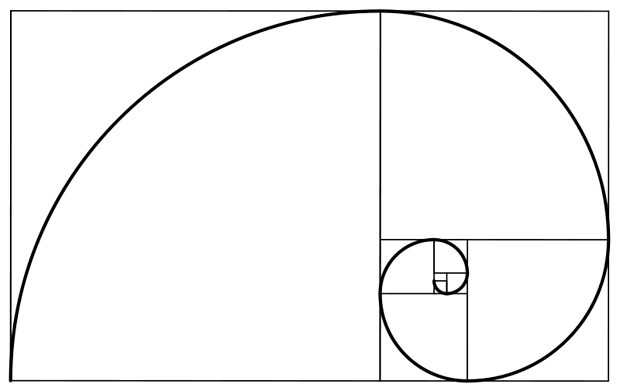
O famoso desenho da espiral de Fibonacci, que você vê abaixo, funciona assim: pegue os dois maiores quadrados da ilustração. Se o quadrado maior, da esquerda, tiver 1,618 cm de lado, então o quadrado da direita, menor, terá 1 cm. Assim, a divisão do tamanho de um pelo outro dá a razão áurea: 1,618… ÷ 1 = 1,618…
A graça é que qualquer par de quadrados que você selecione seguirá a mesma proporção entre si, de modo que o desenho é uma eterna repetição de si mesmo em versões cada vez menores.
A espiral e a sequência de Fibonacci são um easter egg da natureza. Veja algumas de suas aparições ilustres:
Concha do caramujo:
Cada novo pedacinho tem a dimensão da soma dos dois antecessores.
Camaleão:
Contraído, seu rabo é uma das representações mais perfeitas da espiral de Fibonacci.
Elefante:
Se suas presas de marfim crescessem sem parar, ao final do processo, adivinhe qual seria o formato?
Girassol:
Suas sementes preenchem o miolo dispostas em dois conjuntos de espirais: geralmente, 21 no sentido horário e 34 no anti-horário.
Pinha:
As sementes crescem e se organizam em duas espirais que lembram a de Fibonacci: oito irradiando no sentido horário e 13 no anti-horário.
Poesia:
O “número de ouro” aparece até na razão entre as estrofes maiores e menores da Ilíada, épico de Homero sobre os últimos dias da Guerra de Troia.
Partenon:
Os gregos já conheciam a proporção, embora não a fórmula para defini-la. A largura e a altura da fachada deste templo do século V a.C. estão na proporção de 1 para 1,618.
Pirâmides do Egito:
Cada bloco é 1,618 vezes maior que o bloco do nível imediatamente acima. Em algumas, as câmaras internas têm comprimento 1,618 vezes maior que sua largura.
Diagramação:
Vários formatos de cartão de crédito já foram testados. O que se sagrou favorito do público têm laterais na razão de ouro. Fotos em jornais também costumam adotá-la.
Fontes: Roberto Jamal, professor do cursinho Anglo, Claudio Possani, professor do Instituto de Matemática e Estatística da USP.



 Por que existe a letra “h” se ela não tem som?
Por que existe a letra “h” se ela não tem som? 9 filmes imperdíveis para assistir no Prime Video
9 filmes imperdíveis para assistir no Prime Video Filtro de luz azul para telas não tem eficácia comprovada
Filtro de luz azul para telas não tem eficácia comprovada Bactérias “vampiras” letais são atraídas por proteína do sangue humano
Bactérias “vampiras” letais são atraídas por proteína do sangue humano Qual é o modelo de celular mais vendido da história?
Qual é o modelo de celular mais vendido da história?







